The aging mechanism of lithium-ion power batteries is very complex, and there are many coupling factors leading to the performance degradation, which finally make remaining useful life (RUL) prediction a very challenging problem. During the use and maintenance process, the performance of power batteries continues to decline. With the increase of charge and discharge cycles, there is some irreversible chemical reaction occurring inside the power batteries, which results in the charge and discharge capacity attenuation, such as the increase of internal resistance, the decline of capacity and energy and so on. This greatly reduces the driving range of electric vehicles and even brings some safety hazards. Reliable RUL prediction can adequately soothes both anxiety about the unknown driving range and concern about security issues. Ensuring the safe and efficient operation of the power battery pack can also ensure the safety and reliability of the electric vehicle in use to a large extent, reduce failure rate and operating cost, improve user experience, and avoid accidents. As a result, RUL prediction of power batteries is also one of the core contents of power battery management.

RUL of power batteries refers to the number of cycles experienced by which the maximum usable capacity of power batteries degrades to a certain failure threshold under a certain charge and discharge system. RUL prediction is a process of predicting and calculating the remaining useful life of power batteries based on its historical data by certain mathematical means. With the wide application of power batteries in various fields, the RUL prediction technology has been widely concerned and studied. According to the different prediction ideas, the data-driven RUL prediction methods can be further divided into three types: empirical methods, filter-based methods and time series analysis methods.

1. Empirical Methods

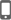
The empirical prediction method assumes that the capacity decline of power battery follows some inherent mathematical relationship, and its parameters are determined by historical data, so a mathematical model describing the aging of power batteries can be established to predict RUL. In order to obtain a reasonable mathematical model, it is usually necessary to use different function forms to repeatedly fit the capacity decay trajectory of power batteries, and the function with the best fitting effect is used to construct the empirical model. The functional forms commonly used as empirical models of power battery life are as follows: the exponential model of Equation (1), the double exponential model of Equation (2), the linear model of Equation (3), the polynomial model of Equation (4), the Verhulst model of Equation (5), etc.

	(1)
	(2)
	(3)
	(4)
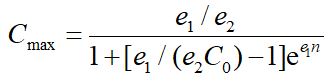	(5)

In Equations (1) to (5), n is the number of equivalent cycles, C_max is the maximum available capacity in the n-th cycle, e is the natural constant, and other parameters are the undetermined coefficients of the model.

he empirical prediction method based on the idea of function fitting has the advantages of simple process and less computation, which is suitable for the scenarios with limited computational resources and low requirement for accuracy. When the RUL prediction program is started, BMS extracts the historical capacity data of the power battery in the memory, and then fits the historical data according to the preset empirical life prediction model to obtain its parameters. Since the aging law of the power battery is completely determined, the prescribed capacity failure threshold (usually 80% of the initial capacity) is substituted into the empirical life prediction model to complete the solution of the power battery RUL.

The empirical fitting method is simple and easy to implement, but it is very sensitive to the fluctuation of sample data, and the prediction results are easy to be scattered. In order to enhance the stability of the algorithm, a filter can be used to eliminate the noise of the sample data, thus forming the filter-based life prediction method.

2. Filter-based life prediction methods

The filter-based life prediction method is the most commonly used method for RUL prediction of power batteries at present. Based on the idea of state estimation, this method takes the undetermined coefficient of the empirical model as model states, and then updates and corrects the state parameters in real time through the observation data. It effectively solves the problem of prediction instability caused by data fitting in the empirical forecasting method.

The filter-based life prediction method uses state space equations to express the aging law of power battery. Taking the double exponential model as an example, four undetermined parameters are selected as the model states, and the state equation is constructed as Equation (6).

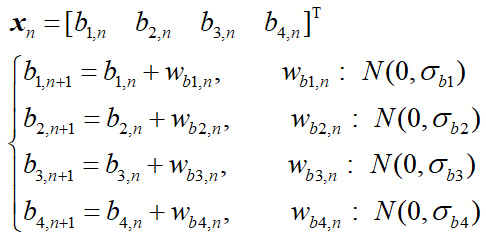(6)

where, x_n is the state vector; wb1~wb4 is the noise with an average value of 0; σb1~σb4 is the variance of parameter noise. The corresponding observation equation is

(7)

where, v_n is the observation noise with an average value of 0, and its variance is σv. After establishing the state space equation, BMS updates and corrects the state variables based on the historical capacity data by using the filtering algorithm to accurately estimate the aging state of power batteries. The following is an example of the extended Kalman filter algorithm to introduce the application of filter-based prediction methods.

The standard Kalman filter algorithm can only solve the state estimation problem of linear systems. Suppose the state space of a linear system is expressed as follows

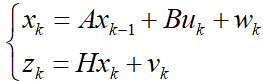(8)

where x is the state variable; A is the state transition matrix; B is the coefficient matrix; H is the observation matrix; k is the equivalent number of cycles, k=0,1,2..., N; N is the length of historical capacity data; w_k and v_k are system noise and observation noise respectively, representing the degree of internal and external disturbance received by the system. We assume that the noise is Gaussian white noise following normal distribution, and the system noise and the observation noise are independent of each other. The covariance matrices of the two are respectively expressed by Q and R, which can characterize the intensity of the noise.

Since Equation (7) is a nonlinear equation, the standard Kalman filter algorithm cannot be directly used to predict the RUL of power batteries. For this reason, the nonlinear system is linearized by Taylor series, and the extended Kalman filter (EKF) algorithm is formed.

The linearized state space equation of Equation (7) is as follows

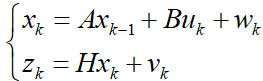(9)

where is the state variable; A is the identity matrix of order 4;.

Fig. 1 shows the state estimation process of the extended Kalman filter algorithm. Firstly, the filter is initialized, that is, the initial parameters and initial state of the filter are set according to the trend of historical data and noise size. The filter then predicts the current states based on the state equation and estimates the covariance of the states. After that, the actual capacity data observed at the current moment is compared with the capacity calculated by the observation equation, and the error is used to correct the states. Repeat the above process to update the filter state recursively. After all the observed data are fed into the filter, the RUL can be obtained by substituting the state estimation results and capacity failure threshold into Equation (7).

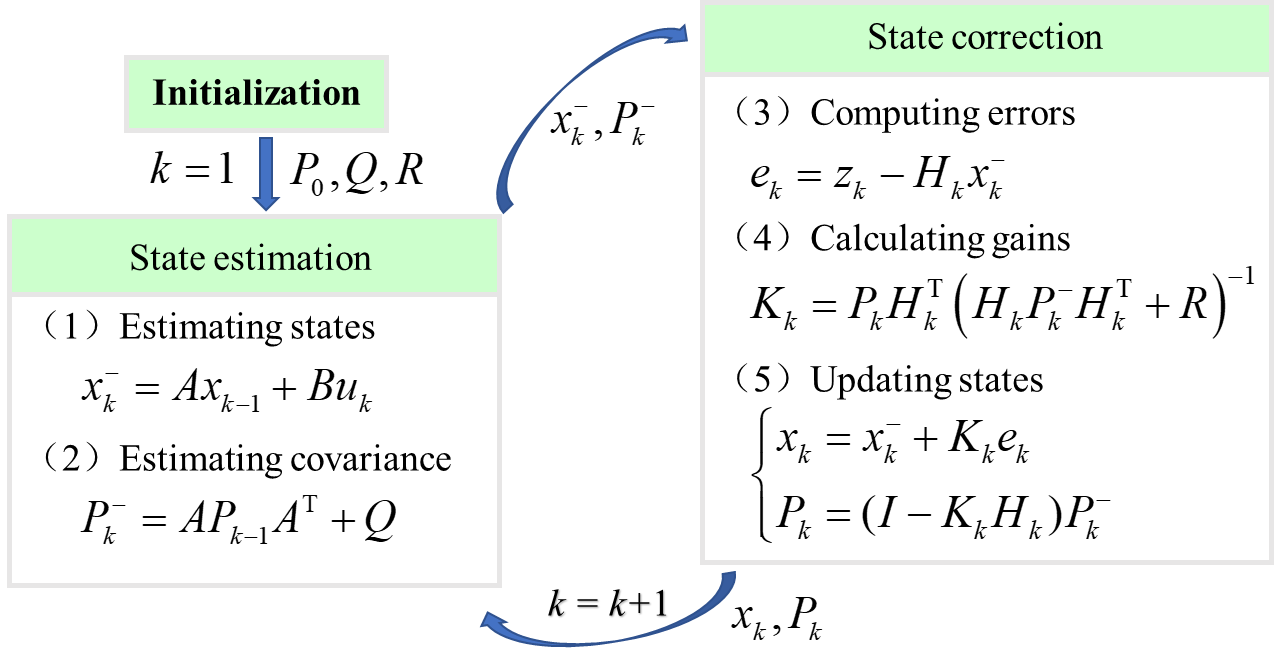
Fig. 1 State estimation process of the Kalman filter algorithm

The RUL prediction result based on the EKF algorithm is shown in Fig. 2. The battery with a whole life of 200 cycles has been used for 100 cycles at present. The historical capacity (i.e. the capacity of the first 100 cycles) is fed into the EKF algorithm one by one to gradually correct the states. At 100 cycles, a double exponential aging model is extrapolated to predict the future capacity trajectory and RUL. The prediction result of RUL based on the EKF algorithm is 127 cycles while the true value is 100 cycles, so the prediction error is 27 cycles with a relative error of 27%.

Fig. 2 prediction results of RUL based on the extended Kalman filter algorithm

3. Time series analysis methods

Different from the above two methods, this method does not rely on a priori empirical model, but takes the capacity decay trajectory of power battery as a time series, analyzes the evolution law of the time series data, predicts the future capacity trajectory, and then obtains RUL of power batteries. The mathematical expression of the time series model is as follows

(10)

Where, function f (·) is the time series model.

Time series model uses the development law of time series to predict the performance of power batteries in the future. Capacity decline of power batteries in use is essentially a long-term time series so that it can be applied in the RUL prediction problems.

It can be seen from Equation (10) that, based on the time series model, the historical capacity observation series between cycles of [n-m, n] can be used to predict the power battery capacity of cycle n+1. The predicted capacity of any cycle can be obtained by recursion of Equation (10). At present, the commonly used time series models for RUL prediction include gray model, autoregressive moving average model, neural network, support vector machine and relevance vector machine and so on. Long short-term memory recurrent neural network (LSTM RNN) is introduced as an example of time series analysis methods.

LSTM RNN is a recurrent neural network with deep learning ability. Its unique logic gate structure enables it to remember long-period features, and has achieved good application effects in machine translation, image recognition and other fields.

Fig. 3 Network structure of LSTM RNN model

The network structure of the LSTM RNN model is shown in Fig. 3. The subscript c of vectors represents the neuron, and the superscript (t) represents the moment t. x(t)represents the input layer at the moment t, and h(t-1) represents the hidden layer at the previous moment t-1. Moment is a commonly used expression of time in the construction of LSTM RNN. For the RUL prediction field of power batteries, it here indicates number of cycles.

The key to LSTM RNN is the internal state sc, which is a linear activation function located at the center of each neuron. The internal state sc has a self-loop with unit weights. The internal state can be used as a carrier for information to be added or removed, and the flow of information can be precisely regulated through a gate structure. The gate is an essential property of the LSTM RNN method and can selectively determine the flow of information. Each gate is a sigmoid function activated by the input layer x(t) and the hidden layer h(t-1) at the previous moment.

Forget Gates: Firstly, the LSTM RNN needs to decide which information needs to be discarded. This decision is made by the sigmoid function layer fc, known as the forget gate. The input of this layer is x(t) and h(t-1) and the output value is between 0 and 1 to determine what happens when each state value is stored in the internal state. 1 indicates that the state value is completely retained, whereas 0 indicates that the state value is completely discarded. For the RUL prediction of power batteries, the discarded information can be capacity data outliers, noise or redundant information from adjacent cycle. The calculation process of forgetting gate is as follows.

(11)

Input Gates and Input Nodes: The next step in determining what information will be stored in the internal states consists of two parts. Firstly, a sigmoid function layer ic known as the input gate decide which value needs to be updated, and then by a tanh function layer gc called the input node produce target state vector , which can be combined with the status value directly. The calculation formula that produces these two outputs is as follows.

	(12)
	(13)

Update the internal state value at the previous time to the current state value :

(14)

Output Gates: Finally, the sigmoid function oc called the output gate determines what information will be output. After going through the tanh function that scaling the value to between -1 and 1, the internal state sc is multiplied by the output of the sigmoid gate to obtain the remaining state value. The expressions are shown in Equations (15) and (16).

	(15)
	(16)

Where the values of W and b are the weight coefficients and deviations of functions of each layer respectively.

Based on the three unique logic gate structures mentioned above, LSTM RNN can effectively learn long-term capacity decline of power batteries and capture the implicit information of historical capacity sequence, so as to achieve accurate prediction of future capacity sequence.

LSTM RNN is used to predict the RUL of a power battery, and results are shown in Fig. 4. LSTM RNN uses the capacity before cycle 253 for training, and predicts the future capacity trajectory in an iterative way until the failure threshold of the power battery was reached. the prediction error of LSTM RNN is only 3 cycles and the relative error is 0.6%. LSTM RNN realizes the accurate prediction of RUL of power batteries.

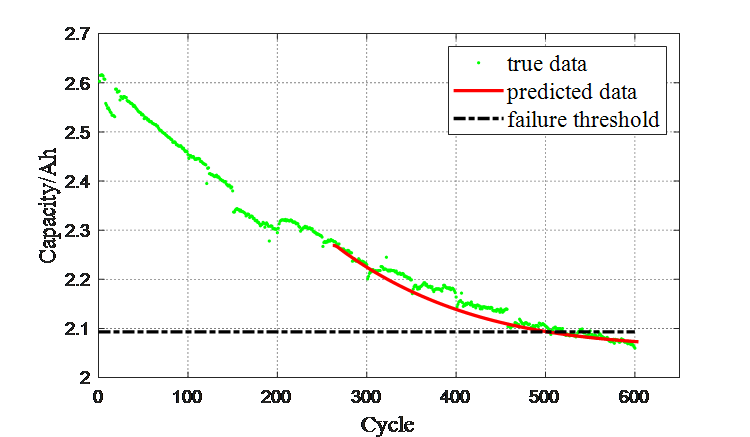
Fig. 4 RUL prediction results based on LSTM RNN

3. References

[1] R. Xiong. Core Algorithms of Battery Management System. Beijing：China Machine Press，2018. (Chinese) (Chapter Six)

[2] R. Xiong, Y. Zhang*, J. Wang, H. He, S. Peng, Michael Pecht, “Lithium-ion battery health prognosis based on a real battery management system used in electric vehicles”, IEEE Transactions on Vehicular Technology, vol. 68, no.5, pp. 4110-4121, May 2019. (Download)

[3] Yongzhi Zhang, Rui Xiong, Hongwen He, Xiaobo Qu, Michael Pecht, “Aging characteristics-based health diagnosis and remaining useful life prognostics for lithium-ion batteries”, eTransportation, vol. 1,pp. 100004, Aug 2019. (Download)

[4] Y. Zhang, R. Xiong*, H. He, and M. Pecht, “Lithium-ion battery remaining useful life prediction with Box–Cox transformation and Monte Carlo simulation”, IEEE Transactions on Industrial Electronics, vol. 66, no.2, pp. 1585-1597, Feb 2019. (Download)

[5] Y. Zhang, R. Xiong*, H. He, and M. Pecht, “Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries”, IEEE Transactions on Vehicular Technology, vol. 67, no. 7, pp. 5695 – 5705, Jul 2018. (Download)

4. Available Resources

(1) Remaining life prediction data: click to download (PDF watermark textbook)