1. SOT estimation

With the rapid development of electric vehicle technology, power battery has been widely used because of its high specific power, high specific energy and other advantages.However, as a fuel substitute, potential safety problems such as fire, smoke and leakage in practical use still seriously hinder the large-scale application of electric vehicles.Therefore, the thermal management of power battery, especially the accurate monitoring of its internal temperature, has become the focus of current research, and is also the core and key of long life, high safety operation.

2. Internal Temperature Estimation of Power Battery Based on Double Kalman Filter Algorithm

The method is divided into two steps: ①By combining the Bernardi cell heat generation model with the heat path heat transfer model, the internal and external temperature of the battery is expressed by using the equation of state analysis, and the discrete time system of temperature is established.②The real-time estimation model of battery internal temperature and environmental parameters is established by using Double Extended Kalman Filter (DKF) to realize the online estimation of battery internal temperature.

Thermal path model

In order to solve the internal temperature of the power battery, the thermal model of the 18650 cylindrical battery was established based on the following assumptions: ①The battery is a uniform heat source;②The battery temperature is uniformly distributed along the axial direction;③Heat is transmitted outwards only in the radial direction.Fig. 1 is the schematic diagram of the thermal circuit model of the power battery. The battery is divided equally along the axial direction and the radial direction n, and each unit has its own thermal resistance and heat capacity.In the axial direction, the thermal resistance and heat capacity of the elements at the same radius are in parallel, while in the radial direction, the thermal resistance and heat capacity of the elements at different radii are in parallel and then in series.

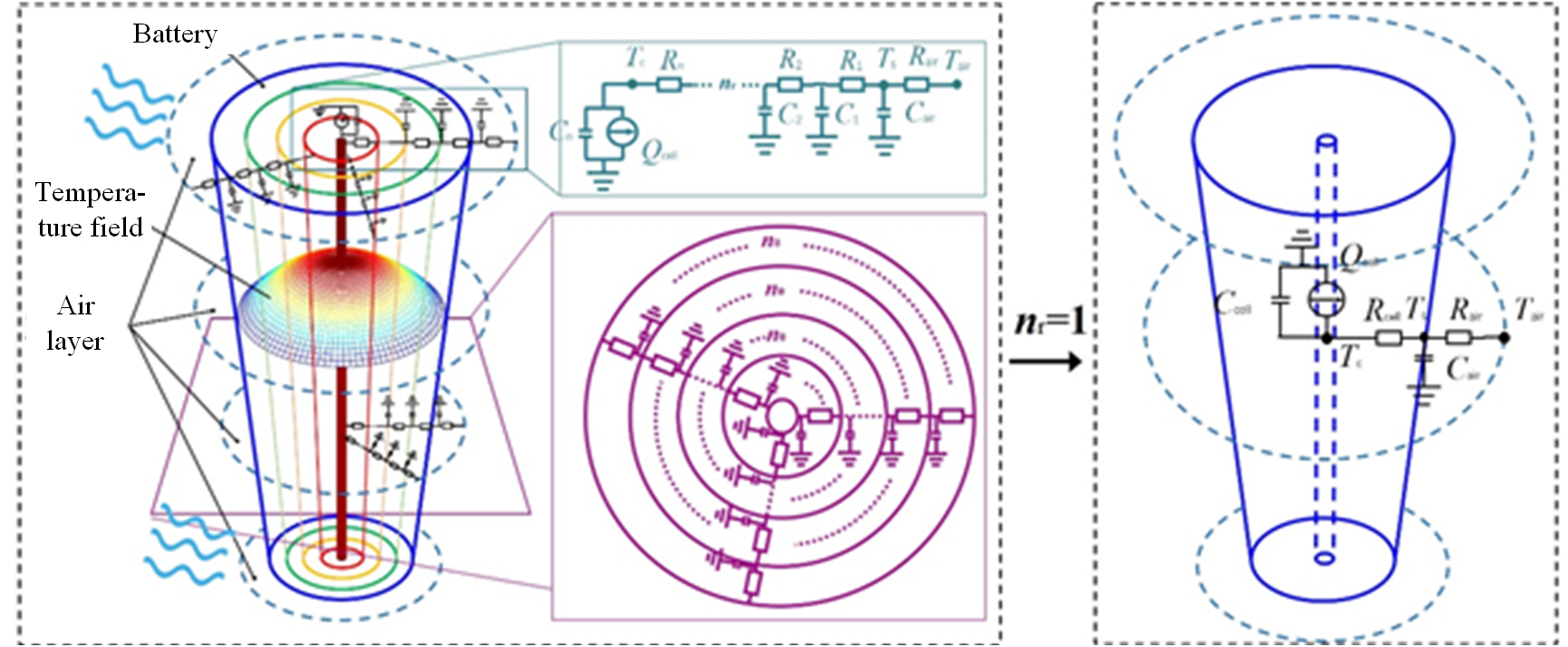
Fig. 1 Schematic diagram of thermal circuit model of power battery

Heat generation model

In essence, different charging and discharging rates will lead to time-varying heat generation rate during the operation of lithium ion power battery with chemical system, which will lead to the difference of temperature inside and outside the battery.Therefore, the calculation and analysis of battery heat source is the basis to obtain its internal temperature.Battery heat generation is affected by temperature, aging, state of charge (SOC) and charge/discharge current.According to the first law of thermodynamics,BERNARDI deduced the heat production expression of the battery:

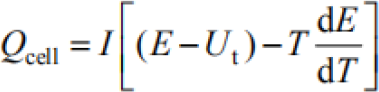(1)

Where, I is the charge and discharge current of power battery;E is the open-circuit voltage of power battery;U_t is the terminal voltage of power battery;T is the power battery temperature (Kelvin temperature);dE/dT is the entropy thermal coefficient of the battery.

The solution of the heat path model

Based on the theory of heat path model, capacitance and resistance are used to describe the heat capacity and heat resistance respectively.The heat source is regarded as the DC source in the circuit.And the temperature is equivalent to the electric potential at that point.Based on the Kirchhoff's law of the circuit model, the solving equation of the thermal circuit model of the power battery is derived.

(2)

It can be obtained by sorting out:

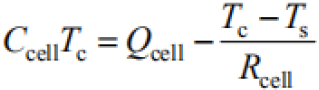	(4)
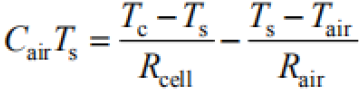	(5)

Let

So:

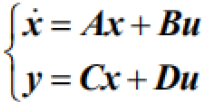(6)

In the formula

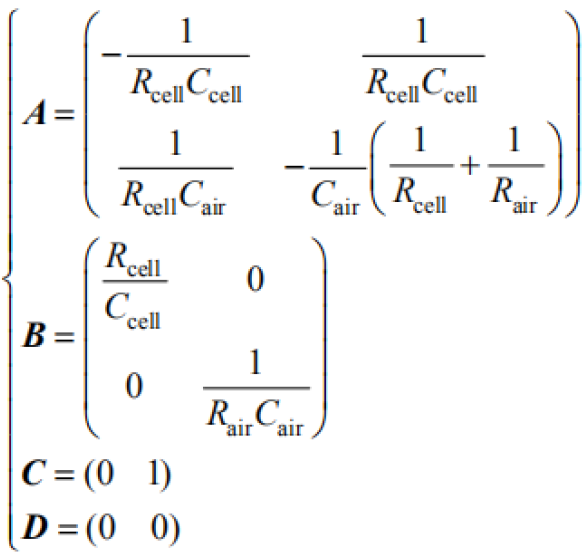(7)

Double extended Kalman filter algorithm

Extended Kalman Filter (EKF) is based on the known model state space equation and noise characteristics, takes the minimum mean square error as the criterion, combines the estimated value at the last moment with the observed value at the current moment to correct, and completes the current state update.The double extended Kalman filter (Dual EKF, DEKF) fuses two simultaneous EKF operations, collaborative state estimation and parameter estimation. Combined with the feedback correction coefficient obtained from the parameter estimator and real-time adjustment of parameter values in the state estimator, the collaborative online estimation of state and parameters is finally realized.The implementation process of DEKF is shown in Figure 2.

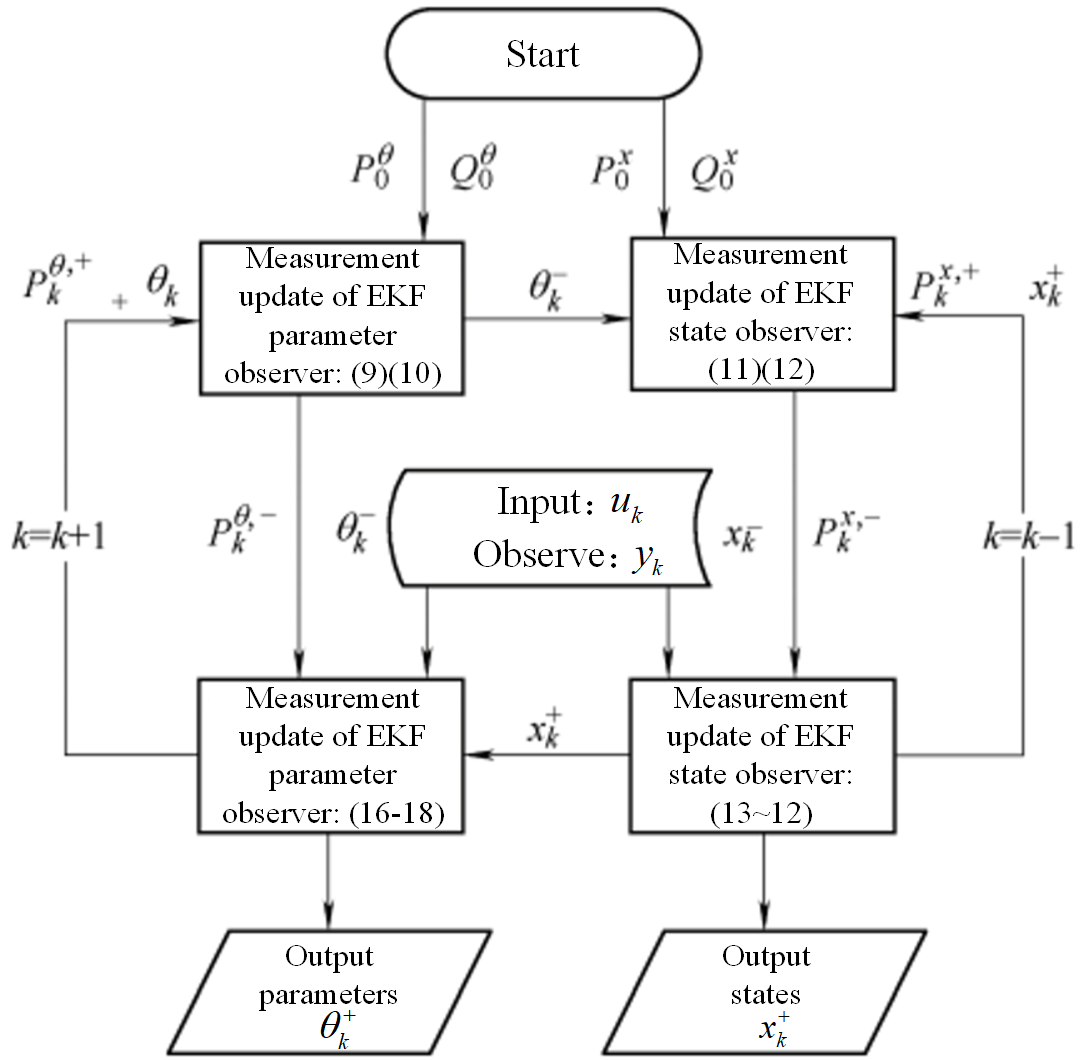
Fig. 2 Flow chart of DEKF calculation

3. Main results

Based on the test platform, seven sets of temperature measurements under charge and discharge conditions were carried out, namely 1C charge, 1C discharge, 2C charge, 2C discharge, 3C charge, 3C discharge and dynamicstest (DST) conditions, to verify the adaptability of the model under different test conditions.

According to the seven groups of test data, the external temperature of the power battery was taken as the observation quantity of the Double extended Kalman Filter algorithm to estimate the internal temperature and heat dissipation characterization parameter RAIR. The obtained test results and simulation estimation results are shown in Fig. 3-6.Referring to the test results in Figure 3-5, the power battery has a large internal temperature rise in the process of charge and discharge. The maximum internal temperature rise of the power battery is around 10-15 ℃ under charge and discharge of 1C, while the maximum internal temperature rise is up to 45℃ when the maximum allowable current is 3C.The results further demonstrate the necessity of on-line estimation of power cell internal temperature.

Fig. 5 Estimated results of internal temperature and heat dissipation characterization parameters of 3C charging

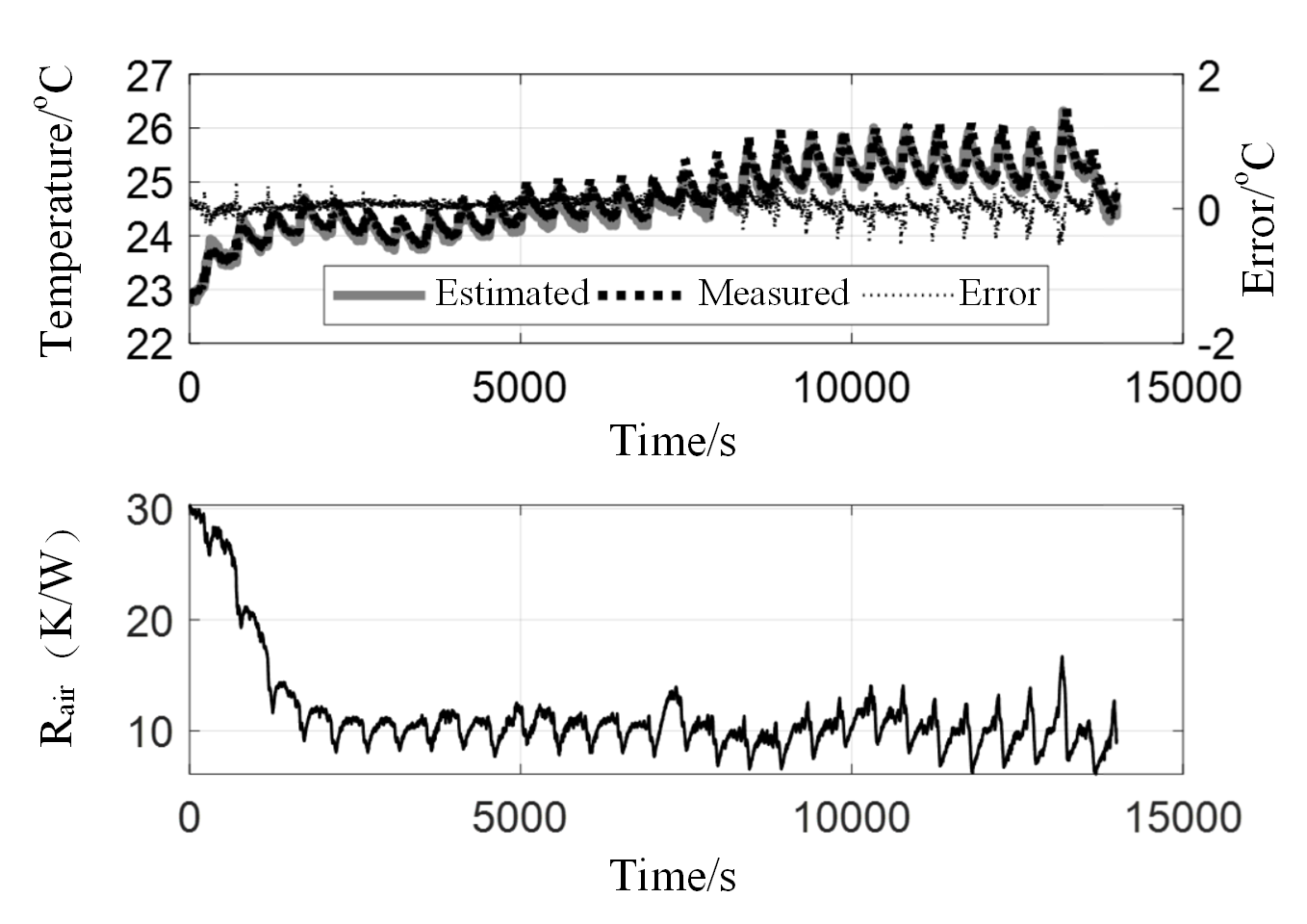
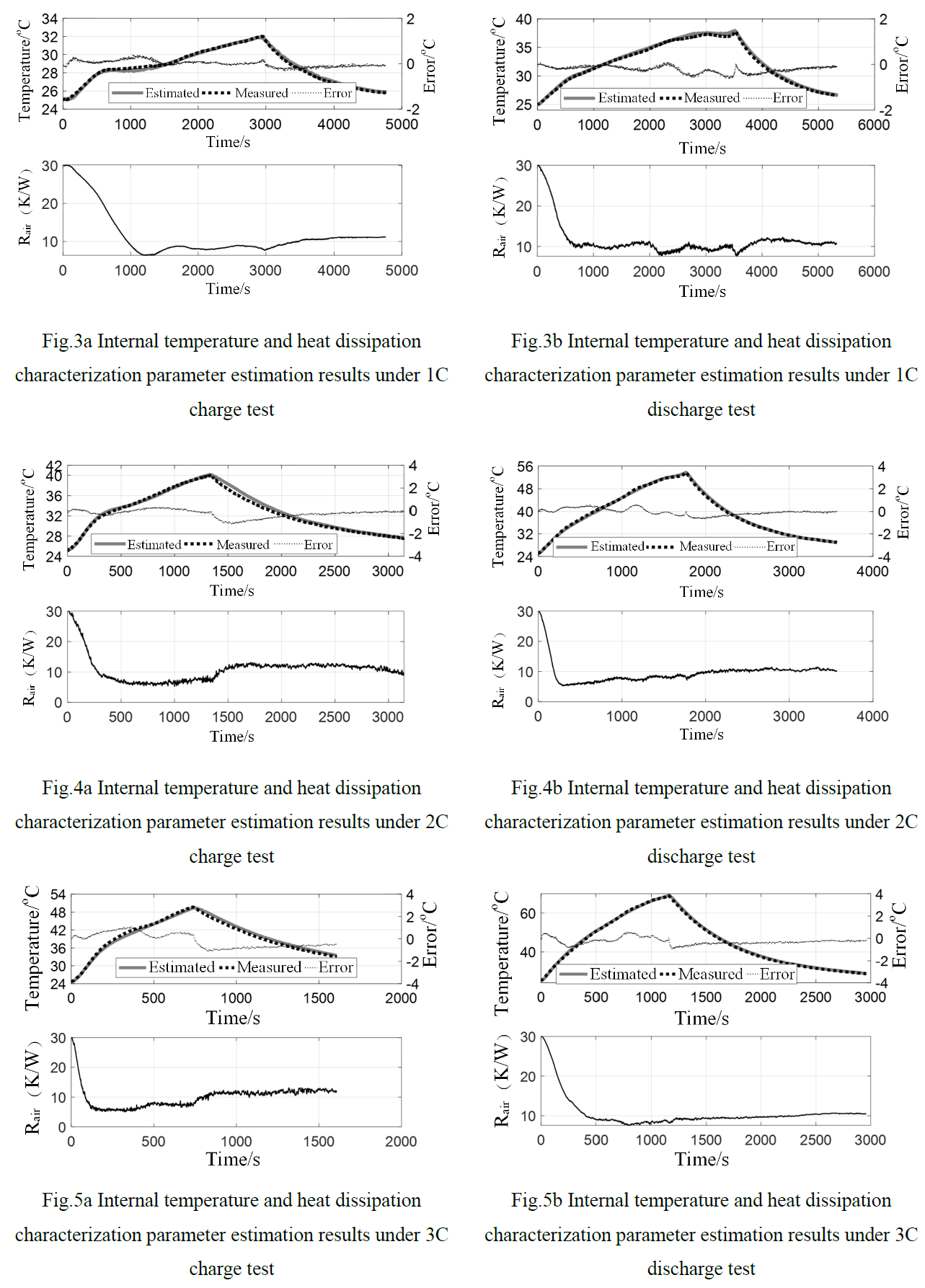
According to the estimation results of the above seven sets of data, the thermal path model has good adaptability to constant current charge-discharge and complex and variable dynamic stress conditions, and the estimation error is less than 1℃.The temperature estimation error is directly proportional to the charge-discharge current rate, which is mainly due to the higher temperature rise at large current, and the corresponding error also increases slightly.It should be noted that the temperature drop stage in Figure 3-5 is the static stage after the battery is charged and discharged. There is no heat input in this process, and the model can still maintain stable estimation ability.

In addition, it can be seen from the estimation results of parameters of the analysis model that the convergence results of the heat dissipation characterization parameter RAIR under different working conditions are basically the same, and the final stability is around 10℃/W.This is because during the test, the power battery was placed in a constant temperature box throughout the test, basically in the same and stable heat dissipation environment, and the value of the heat dissipation characterization parameter Rair should have been similar.On the other hand, it also shows that the model has good adaptability to different working conditions. It not only has stable internal temperature estimation ability, but also can ensure the rationality and authenticity of parameter estimation results.

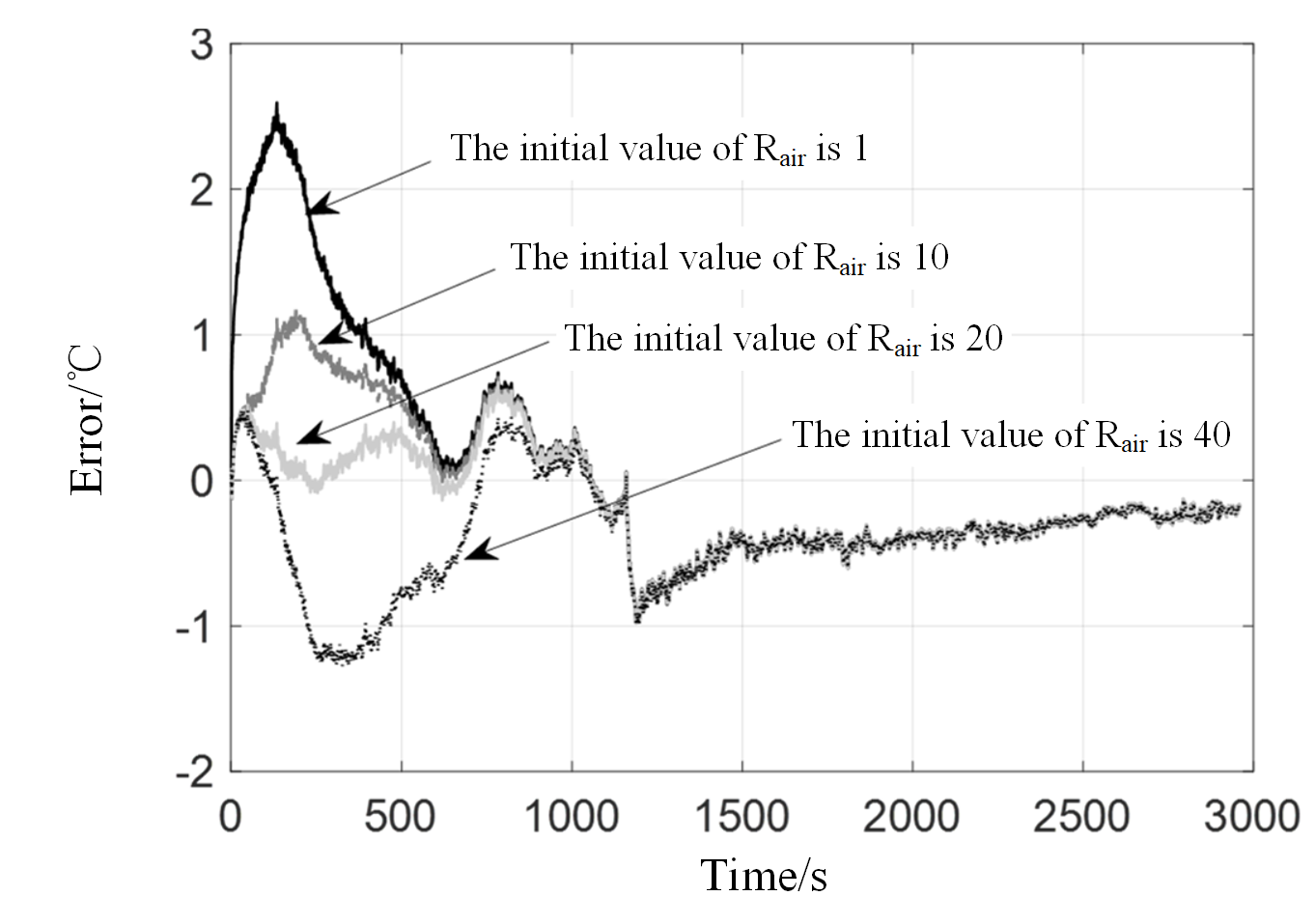
Fig. 7 Curves of temperature estimation error under different initial Rair values

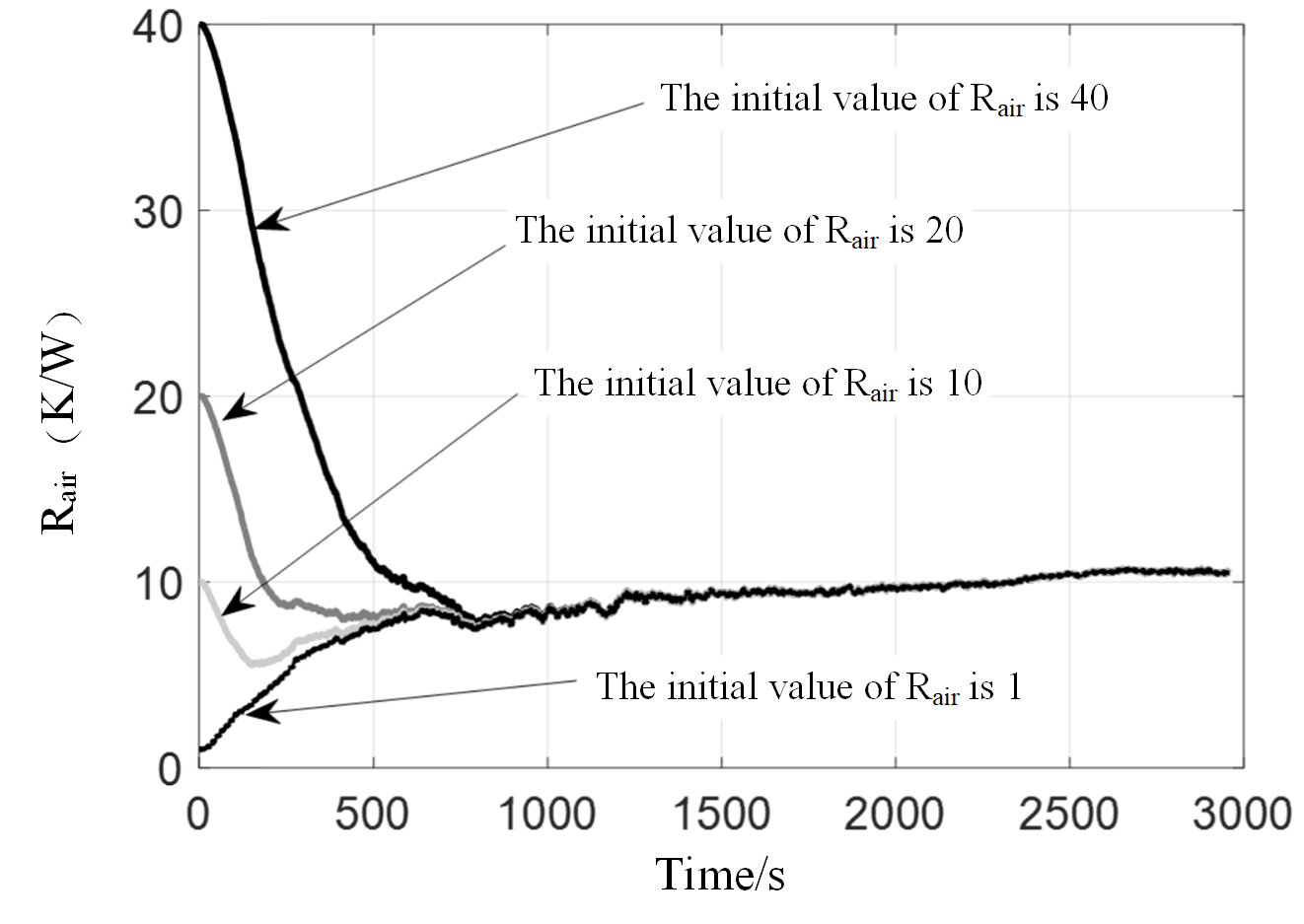
Fig. 8 Changes of Rair at different initial values

Since the heat dissipation characterization parameter RAIR in the model cannot be predicted in advance, the initial value of the input system often has a large deviation. Therefore, it is necessary to further analyze the robustness of the model to the initial value.Fig. 7 and Fig. 8 show the variation curve of temperature estimation error results and RAIR under different initial RAIR values during discharge.They were set as 1℃/W, 10℃/W, 20℃/W and 40℃/W, respectively, and the stability and convergence of the model results were observed.

Thus, cooling characteristic parameter initial value changes, the internal temperature changes of the maximum error of the estimate, the offset degree was mainly affected by Rair initial value deviation degree, and the maximum error are calculated in the initial stage, with the increase of amount of data, Rair gradually converge to the true value of 10℃/W nearby, internal temperature estimation error is reduced.Although the convergence rate of parameter and error is affected by the initial offset, they can converge to the same value in the end.It can be seen that the model has good robustness, and the accurate identification of parameters and the accurate estimation of internal temperature are not affected by the unknown thermal characterization parameters.

4. References

[1] R. Xiong. Core Algorithms of Battery Management System. Beijing：China Machine Press，2018. (Chinese) (Chapter Four)

[2] R. Xiong* and X. Li, “Battery Internal Temperature Estimation Method through Double Extended Kalman Filtering Algorithm”, Journal of Mechanical Engineering, vol. 56, no.14, pp. 146-151, Jul 2020.(Download)

[3] LIN X，PEREZ H E，SIEGEL J B ，et al. Online parameterization of lumped thermal dynamics in cylind rical lithium-ion batteries for core temperature estimation and halth monitoring[J]. IEEE Transactions on Control Systems Technology，2013，21(5)：1745-1755.（Download）

[4] Z. Chen, R. Xiong* , J. Lu and X. Li, “Temperature rise prediction of lithium-ion battery suffering external short circuit for all-climate electric vehicles application”, Applied Energy vol.213, pp. 375-383, Mar 2018. (Download）

[5] CHEN Zeyu，XIONG Rui，SUN Fengchun. Analysis and research status of electric vehicle battery safety accidents[J]. Journal of Mechanical Engineering，2019，55(24)：93-104，116.（Download）