Fractional-order Model

1. Model Introduction

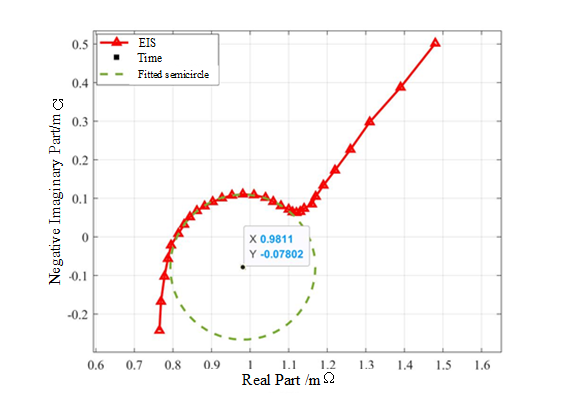
Figure 1 The dispersion effect in electrochemical impedance spectroscopy

Figure 1 shows the EIS test results of a power battery cell. The frequency part is a semicircle with the center below the horizontal axis, which is generally considered to be related to the electric double layer at the interface between the electrode and electrolyte. In fitting this characteristic, researchers found that the equivalent circuit model using pure capacitor components can often not achieve the ideal fitting accuracy. The phenomenon that the measured frequency response of the electric double layer is inconsistent with the pure capacitance is called "dispersion effect". This phenomenon can be fitted by constant phase element (CPE), so the fractional frequency domain model is developed. The impedance expression of constant phase angle element is shown in Table 1.

Table 1 Impedance expression of constant phase angle element

As shown in Table 1, the constant phase angle component has two parameters: the first is Y, its dimension is s^αΩ^-1; the second is α, which is a dimensionless index, used to measure the degree of deviation of the constant phase angle component from the pure capacitive component, 0<α<1. If α=0, the constant phase angle element is a pure resistance element; if α=1, it is a pure capacitive element.

By replacing the pure capacitive element in the Thevenin model with a constant phase angle element, the fractional-order model shown in Figure 2 can be established.

Figure 2 A block diagram of a commonly used fractional frequency domain model structure

In the fractional-order model, the constant phase angle element is often used in parallel with a pure resistance, and its impedance is recorded as Z_arc, and its expression is shown in Table 2. Combine equations (1), (2), and (3), and eliminate Y to get equation (4). From equation (4), it can be found that the arc of the impedance spectrum in Figure 1 can be fitted with this equation. The larger the parameter α, the greater the distance the arc center deviates from the real axis, which also proves that the pure capacitive element (α=1) cannot fit the dispersion effect.

Table 2 The impedance expression of the fractional-order model parallel network

2. Main Formula

The transfer function of the fractional-order model can be expressed as

(1)

Combining the above formulas, we get

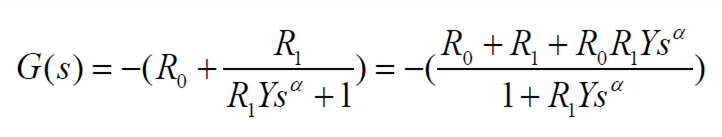(2)

Organizing the above formula, we get

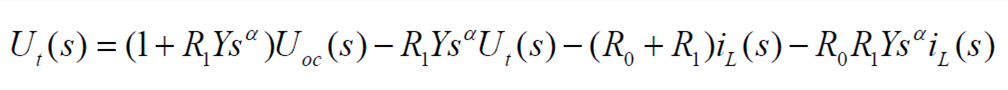(3)

Performing inverse Laplace transform on formula (3), at the k_th sampling time, we get

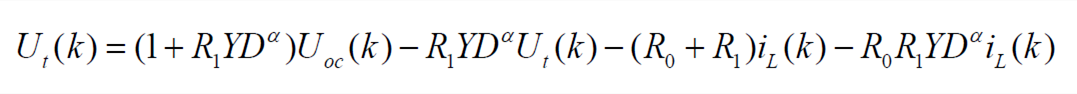(4)

Among them, D_αf(k) represents the fractional calculus/integral to f(k), α>0 represents the fractional differential, and α<0represents the fractional integral. Here, 0<α<1is the fractional differential.

There are three commonly used definitions of fractional differentiation, namely G-L definition, R-L definition and Caputo definition, as shown in Table 3.

Table 3 Commonly used definitions of fractional differential

For most functions, GL definition and RL definition are completely equivalent. Among them, RL definition is the most commonly used in theoretical analysis and research. Caputo definition is more suitable for the description and discussion of initial value problems of fractional differential equations, while GL definition is a discretization approximation. Provides the most direct form and method.

3. Main Results

The model parameter identification is carried out with the DST working condition data of a certain power battery cell under the condition of 40 ℃, and the terminal voltage error identified by α=0.8 is shown in Figure 3. The maximum error of terminal voltage is within 8mV. It can be seen that the fractional-order model also has accurate terminal voltage prediction performance.

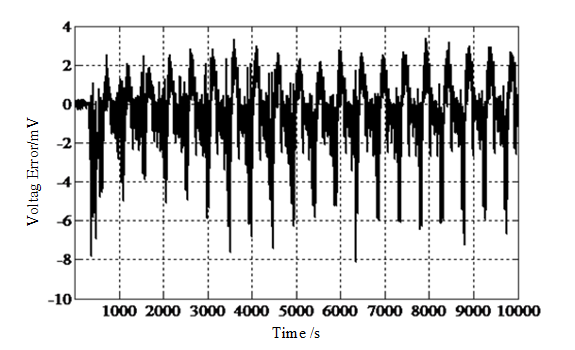
Figure 3 The terminal voltage error of the online identification of the fractional model under DST conditions

4. References

[1] R. Xiong. Core Algorithms of Battery Management System. Beijing：China Machine Press，2018. (Chinese) (Chapter Three Section Three)

[2] J. Tian, R. Xiong, W. Shen and J. Wang, “A Comparative Study of Fractional Order Models on State of Charge Estimation for Lithium Ion Batteries”, Chinese Journal of Mechanical Engineering, vol. 33, pp. 51, July 2020. (Download)

[3] J. Tian, R. Xiong, W. Shen, J. Wang and R. Yang, "Online simultaneous identification of parameters and order of a fractional order battery model", Journal of Cleaner Production, vol. 247, pp. 119147, Feb 2020. (Download)

[4] R. Xiong, J. Tian, W. Shen and F. Sun, "A novel fractional order model for state of charge estimation in lithium ion batteries", IEEE Transactions on Vehicular Technology, vol. 68, no.5, pp.4130- 4139, May 2019. (Download)

[5] H. Mu, R. Xiong, H. Zheng, Y. Chang and Z. Chen, “A novel fractional order model based state-of-charge estimation method for lithium-ion battery”, Appl Energy, vol. 207, pp. 379- 388, DEC 2017. (Download)

5. Available Resources

(1) Fractional model data: Click to download (monograph chapter)